How to factor and expand polynomials

• Factoring and expanding polynomials

You can use five different techniques to factor polynomials. In the first technique, you look for greatest common factors (GCF) in the terms of the polynomial. In the second, you will factor polynomials that are the difference of two perfect squares. In the third, you will be required to factor polynomials that are the sum and difference of two cubes.The fourth technique, called the trinomial factor method, will allow you to factor algebraic expressions that have three terms. The trinomial expressions will be in the form of  ax² ± bx ± c, where a , b and c are real numbers and a ≠ 0. Finally you will be factoring polynomials of four terms by grouping them in pairs in reference to the gcf. These are essentially the five different kinds of polynomial factorization that you are required to be familiar with.

Tips for Factoring Polynomials

Factoring using the greatest common factor:

Definition: The greatest common factor or greatest common divisor of a and b
is the number gcd(a, b) which satisfies three properties:
1. gcd(a, b) > 0
2. gcd(a, b) divides both a and b
3. gcd(a, b) is divisible by every common factor f of a and b
Look for a factor common to every term in the polynomial. Put that factor outside a set of parentheses and the polynomial inside with the factor removed from each term,
e.g. 4x² + 12 = 4(x² + 3)
The gcd is the greatest number that will divide 4x² and 12 simultaneously. We have three factors: 1, 2 and 4. gcd=4. All factoring of this sort can be checked backward by distributing the gcd. The result should  be the original expression. 4 times (x² + 3)= 4x² + 12 (original expression)

Factoring using the difference of two perfect squares: 

Polynomials in the form a² – b² can be factored this way  (a + b)(a − b)

WHEN THE SUM of  two numbers multiplies their difference:

(a + b)(a − b)

-- then the product is the difference of their squares:

(a + b)(a − b) = a² − b²

If you were to FOIL you may note that the the like terms will cancel.

Symmetrically, the difference of two squares can be factored:

x² − 25 = (x + 5)(x − 5)

x² is the square of x.  25 is the square of 5.

Example 1.   Multiply  (x³ + 2)(x³ − 2).

Solution.   Recognize the form:  (a + b)(a − b).  The product will be the difference of two squares:

(x³ + 2)(x³ − 2) = x⁶ − 4.

x⁶ is the square of x³.  4 is the square of 2.

Upon seeing the form (a + b)(a − b), the student should not do the FOIL method.  The student should recognize immediately that the product will be a² − b².

That is skill in algebra.

And the order of factors never matters:

(a + b)(a − b) = (a − b)(a + b) = a² − b².

Problem 1.   Write only final product..

a)	(x + 9)(x − 9) = x2 − 81		b)	(y + z)(y − z) = y2 − z2
c)	(6x − 1)(6x + 1) = 36x2 − 1		d)	(3y + 7)(3y − 7) = 9y2 − 49
e)	(x3 − 8)(x3 + 8) = x6 − 64		f)	(xy + 10)(xy − 10) = x2y2 − 100
g)	(xy2 − z3)(xy2 + z3) = x2y4 − z6		h)	(xn + ym)(xn − ym) = x2n − y2m

Problem 2.   Factor.

a)	x2 − 100  = (x + 10)(x − 10)		b)	y2 − 1 = (y + 1)(y − 1)
c)	1 − 4z2 = (1 + 2z)(1 − 2z)		d)	25m2 − 9n2 = (5m + 3n)(5m − 3n)
e)	x6 − 36 = (x3 + 6)(x3 − 6)		f)	y4 − 144  = (y2 + 12)(y2 − 12)
g)	x8 − y10 = (x4 + y5)(x4 − y5)		h)	x2n − 1 = (xn + 1)(xn − 1)

Problem 3.   Factor completely.

a)  x4 − y4	=	(x2 + y2)(x2 − y2)
	=	(x2 + y2)(x + y)(x − y)

b)  1 − z8	=	(1 + z4)(1 − z4)
	=	(1 + z4)(1 + z2)(1 − z2)
	=	(1 + z4)(1 + z2)(1 + z)(1 − z)

Problem 4.    Completely factor each of the following.  First remove a common factor.  Then factor the difference of two squares.

a)  xy² − xz²  = x(y² − z²) = x(y + z)(y − z)

b)  8x² − 72  = 8(x² − 9) = 8(x + 3)(x − 3)

c)  64z − z³  = z(64 − z²) = z(8 + z)(8 − z)

d)  rs³ − r³s  = rs(s² − r²) = rs(s + r)(s − r)

e)  32m²n − 50n³  = 2n(16m² − 25n²) = 2n(4m + 5n)(4m − 5n)

f)  5x⁴y⁵ − 5y⁵  = 5y⁵(x⁴ − 1) = 5y⁵(x² + 1)(x + 1)(x − 1)

Geometrical algebra

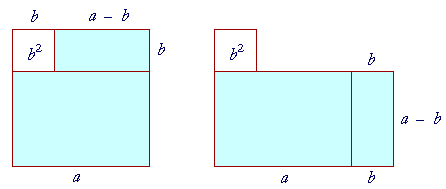
The entire figure on the left is a square on side a.  The square b² has been inserted in the upper left corner, so that the shaded area is the difference of the two squares, a² − b².

Now, in the figure on the right, we have moved the rectangle (a − b)b to the side.  The shaded area is now equal to the rectangle

(a + b)(a − b).

That is,

a² − b² = (a + b)(a − b).

*

The Difference of Two Squares completes our study of products of binomials.  Those products come up so often that the student should be able to recognize and apply each form.

Summary of Multiplying/Factoring

In summary, here are the four forms of Multiplying/Factoring that characterize algebra.

1.  Common Factor		2(a + b)	=	2a + 2b
2.  Quadratic Trinomial		(x + 2)(x + 3)	=	x2 + 5x + 6
3.  Perfect Square Trinomial		(x − 5)2	=	x2 − 10x + 25
4.  The Difference of Two Squares		(x + 5)(x − 5)	=	x2 − 25

Problem 5.   Distinguish each form, and write only the final product.

a)  (x − 3)²  = x² − 6x + 9.   Perfect square trinomial.

b)  (x + 3)(x − 3)  = x² − 9.   The difference of two squares.

c)  (x − 3)(x + 5)  = x² + 2x − 15.   Quadratic trinomial.

d)  (2x − 5)(2x + 5)  = 4x² − 25.   The difference of two squares.

e)  (2x − 5)²  = 4x² − 20x + 25.   Perfect square trinomial.

f)  (2x − 5)(2x + 1)  = 4x² − 8x − 5.    Quadratic trinomial.

Problem 6.   Factor.  (What form is it?  Is there a common factor?  Is it the difference of two squares? .  .  . )

a)  6x − 18  = 6(x − 3).   Common factor.

b)  x⁶ + x⁵ + x⁴ + x³  = x³(x³ + x² + x + 1).   Common factor.

c)  x² − 36  = (x + 6)(x − 6).   The difference of two squares.

d)  x² − 12x + 36  = (x − 6)².   Perfect square trinomial.

e)  x² − 6x + 5  = (x − 5)(x − 1).   Quadratic trinomial.

f)  x² − x − 12  = (x − 4)(x + 3)

g)  64x² − 1  = (8x + 1)(8x − 1)

h)  5x² − 7x − 6  = (5x + 3)(x − 2)

i)  4x⁵ + 20x⁴ + 24x³  = 4x³(x² + 5x + 6) = 4x³(x + 3)(x + 2)

Factoring using the trinomial method: This method requires you to factor the first and third terms and put the factors into the following factored form: ([ ] ± [ ])([ ] ± [ ]). The factors of the first term go in the first position in the parentheses and the factors of the third term go in the second position in each factor, e.g. x² + 2x + 1 = (x + 1)(x + 1).

FACTORING IS THE REVERSE of multiplying.  Skill in factoring, then, depends upon skill in multiplying:  As for a quadratic trinomial --

2x² + 9x − 5

-- it will be factored as a product of binomials:

(?   ?)(?   ?)

The first term of each binomial will be the factors of 2x², and the second term will be the factors of 5.

Now, how can we produce 2x²?  There is only one way:  2x· x :

(2x   ?)(x   ?)

And how can we produce 5?  Again, there is only one way:  1·  5.  But does the 5 go with  2x --

(2x   5)(x   1)

or with  x --

(2x   1)(x   5) ?

Notice:  We have not yet placed any signs

How shall we decide between these two possibilities?  It is the combination that will correctly give the middle term, 9x :

2x² + 9x − 5.

Consider the first possibility:

(2x   5)(x   1)

Is it possible to produce  9x  by combining the outers and the inners:

2x (that is, 2x· 1) with  5x ?

No, it is not.  Therefore, we must eliminate that possibility and consider the other:

(2x   1)(x   5)

Can we produce  9x  by combining  10x  with 1x ?

Yes -- if we choose +5 and −1:

 (2x − 1)(x + 5)

(2x − 1)(x + 5) = 2x² + 9x − 5.

Skill in factoring depends on skill in multiplying -- particularly in picking out the middle term

Problem 1.   Place the correct signs to give the middle term.

a)  2x² + 7x − 15 = (2x − 3)(x + 5)

b)  2x² − 7x − 15 = (2x + 3)(x − 5) 

c)  2x² − x − 15 = (2x + 5)(x − 3) 

d)  2x² − 13x + 15 = (2x − 3)(x − 5) 

Note:  When the constant term is negative, as in parts a), b), c), then the signs in each factor must be different.  But when the constant term is positive, as in part d), the signs must be the same.  Usually, however, that happens by itself.

Nevertheless, can you correctly factor the following?

2x² − 5x + 3  = (2x − 3)(x − 1)

Problem 2.   Factor these trinomials.

a)  3x² + 8x + 5  = (3x + 5)(x + 1)

b)  3x² + 16x + 5  = (3x + 1)(x + 5)

c)  2x² + 9x + 7  = (2x + 7)(x + 1)

d)  2x² + 15x + 7  = (2x + 1)(x + 7)

e)  5x² + 8x + 3  = (5x + 3)(x + 1)

f)  5x² + 16x + 3  = (5x + 1)(x + 3)

Problem 3.    Factor these trinomials.

a)  2x² − 7x + 5  = (2x − 5)(x − 1)

b)  2x² − 11x + 5  = (2x − 1)(x − 5)

c)  3x² + x − 10   = (3x − 5)(x + 2 )

d)  2x² − x − 3   = (2x − 3)(x + 1)

e)  5x² − 13x + 6  = (5x − 3)(x − 2)

f)  5x² − 17x + 6  = (5x − 2)(x − 3)

g)  2x² + 5x − 3  = (2x − 1)(x + 3)

h)   2x² − 5x − 3  = (2x + 1)(x − 3)

i)  2x² + x − 3  = (2x + 3)(x − 1)

j)  2x² − 13x + 21  = (2x − 7 )(x −3)

k)  5x² − 7x − 6  = (5x + 3)(x − 2)

l)  5x² − 22x + 21  = (5x − 7)(x − 3)

Example 1.   1 the coefficient of x².   Factor  x² + 3x − 10.

Solution.   The binomial factors will have this form:

(x   a)(x   b)

What are the factors of 10?  Let us try 2 and 5:

x² + 3x − 10 = (x   2)(x   5).

We must now choose the signs so that the sum of the outers plus the inners will be the middle term, which is +3x.

Choose +5 and −2.

x² + 3x − 10 = (x − 2)(x + 5).

Note:  Since the coefficient of x² is 1, we may simply look for two numbers whose product is 10 and whose sum is 3, the coefficient of x.

But that is only when the coefficient of x² is 1.  In general, the sum of the outers plus the inners must equal the middle term.

(2x − 1)(x + 5) = 2x² + 9x − 5.

Also when the coefficient of x² is 1, then it does not matter in which binomial we put 2 and 5.

(x − 2)(x + 5) = (x + 5) (x − 2).

The order of the factors does not matter.

Example 2.   Factor  x² − x − 12.

Solution.   We must find factors of 12 whose algebraic sum will be the coefficient of x, which is −1.  Choose −4 and + 3:

x² − x − 12 = (x − 4 )(x + 3).

Problem 4.   Factor.  Again, the order of the factors does not matter.

a)  x² + 5x + 6  = (x + 2)(x + 3)

b)  x² − x − 6  = (x − 3 )(x + 2)

c)  x² + x − 6  = (x + 3 )(x − 2)

d)  x² − 5x + 6   = (x − 3)(x − 2 )

e)  x² + 7x + 6  = (x + 1)(x + 6 )

f)  x² − 7x + 6  = (x − 1)(x − 6 )

g)  x² + 5x − 6   = (x − 1)(x + 6 )

h)  x² − 5x − 6   = (x + 1)(x − 6 )

Problem 5.   Factor.

a)   x² − 10x + 9  = (x − 1 )(x − 9)

b)  x² + x − 12  = (x + 4)(x − 3)

c)  x² − 6x − 16  = (x − 8)(x + 2)

d)  x² − 5x − 14   = (x − 7)(x + 2)

e)  x² − x − 2  = (x + 1)(x − 2)

f)  x² − 12x + 20  = (x − 10 )(x − 2)

g)  x² − 14x + 24  = (x − 12 )(x − 2)

Example 3.   Factor completely  6x⁸ + 30x⁷ + 36x⁶.

Solution.   To factor completely means to first remove any common factors (Lesson 15).

6x8 + 30x7 + 36x6	=	6x6(x2 + 5x + 6).
Now continue by factoring the trinomial:
	=	6x6(x + 2)(x + 3).

Problem 6.   Factor completely.  First remove any common factors.

a)  x³ + 6x² + 5x  = x(x² + 6x + 5) = x(x + 5)(x + 1)

b)  x⁵ + 4x⁴ + 3x³  = x³(x² + 4x + 3) = x³(x + 1)(x + 3)

c)  x⁴ + x³ − 6x²  = x²(x² + x − 6) = x²(x + 3)(x − 2)

d)  4x² − 4x − 24  = 4(x² − x − 6) = 4(x + 2)(x − 3)

e)  6x³ + 10x² − 4x  = 2x(3x² + 5x − 2) = 2x(3x − 1)(x + 2)

f)  12x¹⁰ + 42x⁹ + 18x⁸  = 6x⁸(2x² + 7x + 3) = 6x⁸(2x + 1)(x + 3).

2nd Level

Example 4.   Factor by making the leading term positive.

−x² + 5x − 6 = −(x² − 5x + 6) = −(x − 2)(x − 3).

Problem 7.   Factor by making the leading term positive.

a)   −x² − 2x + 3  = −(x² + 2x − 3) = −(x + 3)(x − 1)

b)   −x² + x + 6  = −(x² − x − 6) = −(x + 2)(x − 3)

c)   −2x² − 5x + 3  = −(2x² + 5x − 3) = −(2x − 1)(x + 3)

Quadratics in different arguments

Here is the form of a quadratic trinomial with argument x :

ax² + bx + c.

The argument is whatever is being squared.  x is being squared.  x is called the argument.  The argument appears in the middle term.

a, b, c are called constants.  In this quadratic,

3x² + 2x − 1,

the constants are  3, 2, −1.

Now here is a quadratic whose argument is x³:

3x⁶ + 2x³ − 1.

x⁶ is the square of x³.  (Lesson 13:  Exponents.)

But that quadratic has the same constants -- 3, 2, − 1 -- as the one above.  In a sense, it is the same quadratic only with a different argument. For it is the constants that distinguish a quadratic.
Now, since the quadratic with argument x can be factored in this way:

3x² + 2x − 1 = (3x − 1)(x + 1),

then the quadratic with argument x³is factored in the same way:

3x⁶ + 2x³ − 1 = (3x³ − 1)(x³ + 1).

Whenever a quadratic has constants 3, 2, −1, then for any argument, the factoring will be

(3 times the argument − 1)(argument + 1).

Example 5.		z2 − 3z − 10	=	(z + 2)(z − 5).
		x8 − 3x4 − 10	=	(x4 + 2)(x4 − 5).

The trinomials on the left have the same constants   1, −3, −10   but different arguments.  That is the only difference between them.  In the first, the argument is z.  In the second, the argument is x⁴.

(The square of x⁴ is x⁸.)

Each quadratic is factored as

(argument + 2)(argument − 5).

Every quadratic with constants  1, −3, −10  will be factored that way.

Problem 8.

a)  Write the form of a quadratic trinomial with argument z.

az² + bz + c

b)  Write the form of a quadratic trinomial with argument x⁴.

ax⁸ + bx⁴ + c

c)  Write the form of a quadratic trinomial with argument xⁿ.

ax²ⁿ + bxⁿ + c

Problem 10.   Multiply out each of the following, which have the same constants, but different argument.

a)

(z + 3)(z − 1) = z2 + 2z − 3

b)

(y + 3)(y − 1) = y2 + 2y − 3

c)  (y⁶ + 3)(y⁶ − 1)  = y¹² + 2y⁶ − 3

d)  (x⁵ + 3)(x⁵ − 1)  = x¹⁰ + 2x⁵ − 3

Problem 11.   Factor each quadratic.

a)  x² − 6x + 5  = (x − 1)(x − 5)

b)  z² − 6z + 5  = (z − 1)(z − 5)

c)  x⁸ − 6x⁴ + 5  = (x⁴ − 1)(x⁴ − 5)

d)  x¹⁰ − 6x⁵ + 5  = (x⁵ − 1)(x⁵ − 5)

e)  x⁶y⁶ − 6x³y³ + 5  = (x³y³ − 1)(x³y³ − 5)

Problem 12.   Factor each quadratic.

a)  x⁴ − x² − 2 = (x² − 2)(x² + 1)

b)  y⁶ + 2y³ − 8 = (y³ + 4)(y³ − 2)

c)  z⁸ + 4z⁴ + 3 = (z⁴ + 1)(z⁴ + 3)

d)  2x¹⁰ + 5x⁵ + 3 = (2x⁵ + 3)(x⁵ + 1)

e)  x⁴y² − 3x²y − 10 = (x²y + 2)(x²y − 5)